Big-O는 알고리즘의 성능을 수학적으로 표현해주는 표기법이다.
이것으로 알고리즘의 시간과 공간 복잡도를 표현할 수 있다.
시간과 공간 복잡도의 표현을 통해 정확한 알고리즘 시간을 산출하기보다,
데이터나 요청의 증가율에 따른 성능을 예측하는 것을 목표로 한다.
Big-O 표기법을 알바오자.
먼저, 첫번째로 O(1)알고리즘이 있다.
이 알고리즘은 입력데이터의 크기와 상관없이 일정한 시간이 걸리는 알고리즘을 말한다.

위의 예와 같이 어떠한 데이터가 들어와도 동일한 시간이 걸리는 것을 보증한다.
이러한 경우를 O(1) 시간복잡도를 가진다고 표현한다.
그래프로 표현하면 아래와 같다.

두번째로, O(n)알고리즘이 있다.
O(n)알고리즘은 입력 데이터의 크기에 비례해서 처리시간이 걸리는 알고리즘을 표현한다.
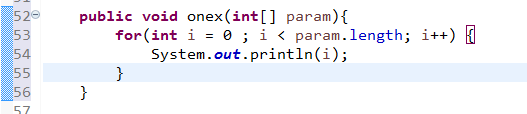
위의 예와 같이 전달받는 데이터의 길이에 따라 처리시간이 일정하게 늘어나게 된다.
언제나 데이터가 증가함에 따라 비례해서 처리시간도 증가하기 때문에 아래와 같은 그래프로 표현한다.
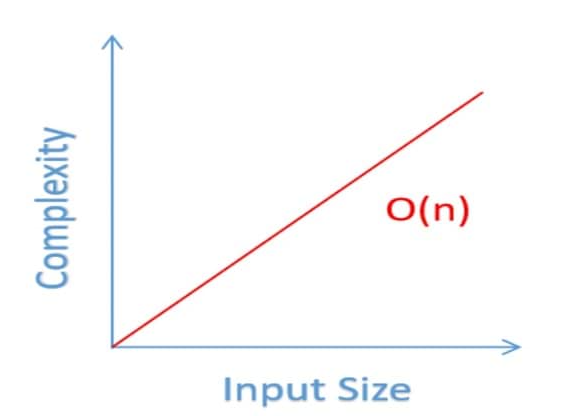
세번째론, O(n²)알고리즘이 있다.
O(n²)은 간단하게 O(n)에서 n을 한번 더 돌린 경우라고 할 수 있다.

위의 예와 같이 데이터의 길이만큼 한번 더 돌기 때문에 제곱의 형태가 된다.
흔히 볼 수 있는 큐브의 한면적을 상상하면 된다.
예를 들어 길이가 3인 데이터가 들어왔으면 3의 제곱만큼 돌기 때문에 3x3의 큐브의 한면을 상상해 볼 수 있다.
여기서 데이터의 길이가 늘어나면(데이터가 커질수록) 그 제곱만큼 확장한다고 보면 된다.
따라서, 처리시간에 부담도 점점 커지게 되며 아래와 같은 그래프로 표현한다.
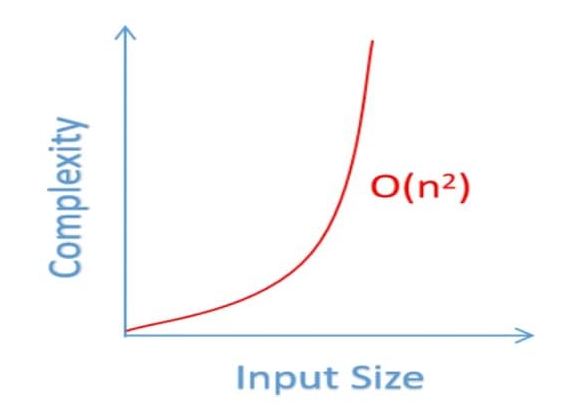
처음에는 사이즈가 작으니 처리시간이 적게 걸리지만, 나중에 데이의 길이가 많으 늘어나있을때는,
하나의 길이만 추가되어도 엄청나게 부담이되어 그래프가 수직상승이 되어진다.
네번째론, O(nm)알고리즘이 있다.
O(n²)은 n을 n만큼 돌린 경우라고 한다면, O(nm)은 n을 m만큼 돌린 경우라 볼 수 있다.

위와 같이 n을 m만큼 돌리기 때문에, 데이터의 길이에 따라 처리시간이 점점 늘어나게 된다.
따라서 그래프의 모양도 O(n²)과 비슷하다.
다섯번째론, O(n³)알고리즘이 있다.
간단하게, O(n²)에서 n을 한번 더 돌린 경우라 볼 수 있다.
위의 O(n²)은 정사각형 큐브의 한면이라고 예시를 들었다.
O(n³)은 O(n²)에서 n만큼을 더 곱하기 때문에 높이가 생긴
정사각형큐브 그 자체라고 생각하면 된다.
소스로 표현하면 아래와 같다.
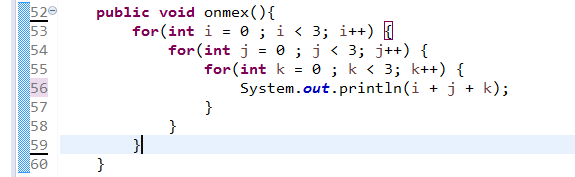
데이터가 증가함에 따라 당연히 처리시간은 O(n²)에서 n만큼 한번 더 돌리기때문에 O(n²)보다 월등히 오래 걸리게 된다.
그래프는 O(n²)이 위로 조금 더 가파른 모양을 하게 된다.
여섯번째론, O(2ⁿ)알고리즘이 있다.
O(2ⁿ)은 피보나치수열이라 보면 된다.
1, 1, 2, 3, 5, 8 과 같이 한 면적에 정사각형을 계속 붙여나가는 형태라 볼 수 있다.
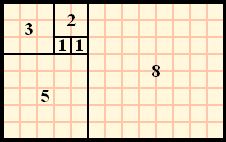
피보나치를 소스로 표현하면 아래와 같다.

즉, 매번 함수를 호출할 때마다 2번씩 다시 호출하는데, 이걸 트리의 높이만큼 반복하는 것이다.
그래프로보면 O(n³)보다 시간이 더 오래 걸리게 된다.

마지막으로, O(log n) 알고리즘이 있다.
O(log n)의 대표적인 알고리즘은 이진검색이 있다.
이진검색은 키값과 데이터의 중간값을 비교하며 절반은 검색영역에서 제외시키면 데이터를 비교하는 형태다.
소스로 표현하면 아래와 같다.

순차검색에 비해서, 절반씩 데이터를 검색영역에서 지워나가기 때문에 속도가 빠른편이다.
데이터가 증가해도 성능이 크게 차이가 나지 않는다.
정리해서 Big-O표기법의 속도그래프를 아래와 같이 볼 수 있다.

'자료구조 > 🧩자료구조' 카테고리의 다른 글
| DataBase Index에서 기본적으로 HashTable이 아닌 B-Tree를 쓰는 이유 (0) | 2023.01.09 |
|---|

댓글